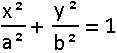 tekent
men een ingeschreven rechthoek (zijden evenwijdig met de assen).
tekent
men een ingeschreven rechthoek (zijden evenwijdig met de assen).Wat is de oppervlakte van de grootste rechthoek die je in deze ellips kan inschrijven ?
 ab
ab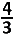 ab
ab ab
ab
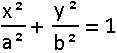 tekent
men een ingeschreven rechthoek (zijden evenwijdig met de assen). tekent
men een ingeschreven rechthoek (zijden evenwijdig met de assen).Wat is de oppervlakte van de grootste rechthoek die je in deze ellips kan inschrijven ? |
A.  ab ab |
|---|---|
| B. 2ab | |
| C. ab | |
D. 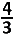 ab ab | |
E.  ab ab |
[ 6-8129 - op net sinds 2.1.2018-(E)-2.11.2023 ]
|
IN CONSTRUCTION Area oh the greatest possible rectangle |
A. ½ab |
|---|---|
| B. 2ab | |
| C. ab | |
D. 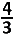 ab ab | |
| E. |