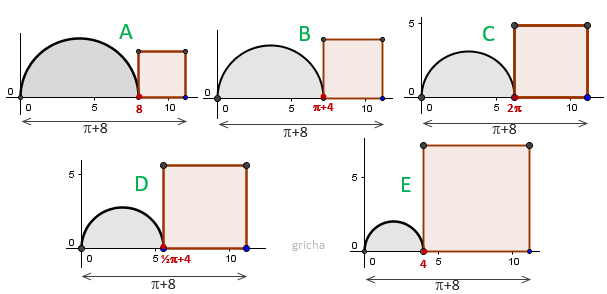
1^ste manier :
Bereken voor elke figuur de oppervlakte van de halve cirkel en van het vierkant. Na optelling zal blijken welk getal het kleinst is.
2^de manier :
Noem x de abscis van het snijpunt van de halve cirkel en het vierkant zodat  x  de straal is van de cirkel en  (π + 8) − x  de lengte van de zijde van het vierkant.
We moeten dus nagaan voor welke x de som S van de twee oppervlaktes het grootst is. Die oppervlakte S is in functie van x gelijk aan
\(S=\frac12\pi\left(\frac {x}2\right)+(\pi+8-\pi)^2=\frac{\pi}8x^2+\pi^2+8^2+x^2+16\pi-2\pi x-16x\\ =\left(\frac{\pi}8+1\right)x^2-2(\pi+8)x+16\pi+\pi^2+64 \)
Deze kwadratische uitdrukking heeft zeker een minimum want de coëfficiënt van x² is gelijk aan \(\frac {2(\pi+8)} {2\left(\frac{\pi}8+1\right)}=8 \)