van (
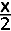 - 2)²
- 2)²zijn dezelfde
als deze van
|
De nulwaarde(n) van ( 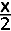 - 2)² - 2)²zijn dezelfde als deze van |
A. x² − 8x + 16 |
|---|---|
| B. 4 − 4x + x² | |
| C. 4 − ¼ x² | |
| D. 4 + ¼x² | |
| E. 4 − 2x + ¼ x² |
[ 3-8122- op net sinds 9.9.16-()-27.10.2023 ]
| IN CONSTRUCTION | A. |
|---|---|
| B. | |
| C. | |
| D. | |
| E. |