Wiskunde Multiple Choice Vraag uit Gricha's Wiskundige Vragenbank

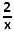
Voor welke functie f is f (a + b) = f (a) + f (b) ? ( voor alle a > 0 en b > 0 )	A. f (x) = x + 1
	B. f (x) = x²
	C. f (x) =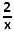
	D. f (x) = x
	E. f (x) = -5x

[ 4-8111 - op net sinds 22.9.16-(E)-20.3.2024 ]

Translation in E N G L I S H

For which function f is f (a + b) = f (a) + f (b) ? ( for all real a, b )	A. f (x) = x + 1
	B. f (x) = x²
	C. f (x) =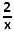
	D. f (x) = x
	E. f (x) = -5x

Oplossing - Solution

A, B, C, D niet want bv. voor B is
f(a + b) = (a + b)²
f(a) + f(b) = a² + b²
en ... (a + b)² ≠ a² + b²
E wel want
f(a + b) = − 5(a + b)
f(a) + f(b) = − 5a − 5b
en die zijn wel gelijk wegens de distributieve eigenschap