De driehoeken
APD en PQD zijn


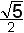
|
De driehoeken APD en PQD zijn |
A. congruent |
|---|---|
| B. niet gelijkvormig | |
C. gelijkvormig met factor  | |
D. gelijkvormig met factor  | |
E. gelijkvormig met factor 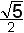 |
[ 3-8099 - op net sinds 21.9.16-(e)-27.8.2025 ]
|
IN CONSTRUCTION Triangles APD en PQD similar (?) with factor ... |
A. |
|---|---|
| B. | |
| C. | |
| D. | |
| E. |
