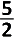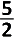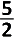De veelterm
V(x) = 2x³ + ax² + bx + 3
heeft drie nulwaarden
waaronder −1 en +1.
Wat is de derde nulwaarde ?
|
A.  |
|---|
| B. 2 |
C. 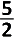 |
| D. 3 |
| E. − 3 |
[ 3,4-8095 - op net sinds 24.3.2017-(E)-6.12.2024 ]
Translation in E N G L I S H
The polynomial
V(x) = 2x³ + ax² + bx + 3
has three zero's :
−1, 1 and ..?
|
A.  |
|---|
| B. 2 |
C. 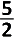 |
| D. 3 |
| E. − 3 |
Oplossing - Solution
1ste manier : zonder de waarde van a en b te berekenen
Elke veelterm met drie nulwaarden x1, x2 en x3 kan geschreven worden als
p(x − x1)(x − x2)(x − x3).
Als twee nulwaarden −1, +1 gekend zijn :
V(x) = p(x +1)(x − 1)(x − x3) = 2x³ + ax² + bx + 3
Uit de gelijkheid van de termen van de derde macht volgt : p = 2
Uit de gelijkheid van de termen van de nulde macht volgt : p.x3 = 3
Hieruit volgt onmiddellijk dat \(x_3=\frac32\)
2de manier : door eerst a en b te berekenen
Wegens de reststelling moet V(−1) = V(1) = 0.
Dus −2 + a − b + 3 = 0 ∧ 2 + a + b + 3 = 0 ⇔ a − b = −1 ∧ a + b = − 5
Door optelling verkrijgen we 2a = − 6 ⇔ a= − 3
Door aftrekking verkrijgen we −2b = 4 ⇔ b = −2
De veelterm V(x) is dus 2x³ − 3x² − 2x + 3 die we nu delen door x + 1
Quotiënt vinden we met de regel van Horner:
| 2 −3 −2 3
−1 | −2 5 −3
| 2 −5 3 0
zodat V(x) = (x + 1)(2x² − 5x + 3) = (x + 1)(x − 1)(2x − 3)
We weten immers dat 2x² − 5x + 3 deelbaar moet zijn door x − 1
Uit de laatste factor kunnen we concluderen dat \(\frac32\) de derde nulwaarde is
3de manier : zonder de waarde van a en b te berekenen
We delen 2x³ + ax² + bx + 3 direct door x + 1 (en de rest MOET nul zijn)
| 2 a b 3
−1 | −2 2−a a−b−2
| 2 a−2 2+b−a a−b+1 (=rest)
Door het feit dat a−b+1=0 is b−a=1 en dus 2 + b − a = 2 + 1 = 3
Bijgevolg is V(x) = (x + 1)(2x² + (a−2)x² + 3) = (x + 1)(x − 1)(2x − 3) want wederom
weten we dat 2x² + (a−2)x² + 3 MOET deelbaar zijn door x − 1
Uit de laatste factor kunnen we concluderen dat \(\frac32\) de derde nulwaarde is