Wiskunde Multiple Choice Vraag uit Gricha's Wiskundige Vragenbank

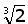
Een gelijkbenige driehoek wordt gevormd door de oorsprong O, het punt A en de top T. (zie figuur) Voor welke a ( > 0 ) is de oppervlakte van ΔOAT het grootst ?	A. 1
B.
C.
D.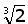
E.

IN CONSTRUCTION max area of ΔOAT for a = ?	A.
B.
C.
D.
E.

We drukken eerst de oppervlakte S uit in functie van a : $S=\frac12.2a.\frac{a}{1+a^3}=\frac{a^2}{1+a^3}$ .
Om S te kunnen maximaliseren berekenen we de afgeleide van S naar a :
$\\\mathbf{D_a}\:S=\frac{2a(1+a^3)-a^2.3a^2}{(1+a^3)^2}=\frac{2a+2a^4-3a^4}{(1+a^3)^2}=\frac{2a-a^4}{(1+a^3)^2}=\frac{a(2-a^3)}{(1+a^3)^2}$
Omdat er maar één strikt positieve nulwaarde is voor die afgeleide (nl. ∛2 ) kunnen we nu al vermoeden dat dit het antwoord zal zijn. Om dit vermoeden te bevestigen maken we een tekenschema van D_aS.
Het teken van D_aS wordt volledig bepaald door de teller van D_a S, nl. a(2 − a³).
De noemer is immers steeds positief.