4.sin³x + 2.sin²x − 2.sinx − 1 = 0
⇔ 4t³ + 2t² − 2t − 1 = 0  ∧  t = sin x
⇔ 2t²(2t + 1) − (2t + 1) = 0  ∧  t = sin x
⇔ (2t² − 1)(t + 1) = 0  ∧  t = sin x
⇔ (t − 1)(t + 1)(2t + 1) = 0  ∧  t = sin x
We lossen afzonderlijk op :
  a) t − 1  ∧  t = sin x  ⇔  sinx = 1  ⇔  sin x =
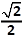
  → twee oplossingen tussen 0° en 360°
  b) t + 1  ∧  t = sin x  ⇔  sinx = −1  ⇔  sin x = − 
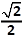
  → twee oplossingen tussen 0° en 360°
  c) 2t + 1 = 0  ∧  t = sin x  ⇔  2sin x = −1  ⇔  sin x =
  → twee oplossingen tussen 0° en 360°
Vermits en geen overlappingen zijn tussen deze zes oplossingen is zes dus ook het juiste antwoord.