?
Het vierkant met zijde 6 cm is verdeeld in
vier congruente vierkanten met zijde 3 cm. Als je willekeurig twee van de negen
roosterpunten kiest, wat is dan de kans dat de afstand tussen die twee punten
G E E N geheel aantal cm is ?
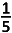
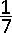
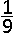
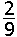

|
?
Het vierkant met zijde 6 cm is verdeeld in
vier congruente vierkanten met zijde 3 cm. Als je willekeurig twee van de negen
roosterpunten kiest, wat is dan de kans dat de afstand tussen die twee punten
G E E N geheel aantal cm is ?
|
A. 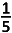 |
|---|---|
B. 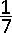 | |
C. 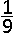 | |
D. 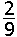 | |
E.  |
[ 6-8068 - op net sinds 20.12.2023-(E)-26.5.2024 ]
|
IN CONS IN CONSTR IN CONSTRUC IN CONSTRUCTI IN CONSTRUCTION |
A. |
|---|---|
| B. | |
| C. | |
| D. | |
| E. |
