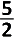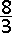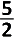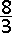Wat is de kleinste waarde die

kan aannemen tussen de twee verticale asymptoten van de kromme ?
|
A. 0 |
|---|
| B. 1 |
C.  |
D. 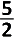 |
E. 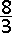 |
[ 5-8049 - op net sinds 21.10.2020-(E)-5.12.2023 ]
Translation in E N G L I S H
What is the smallest value

can assume between the two
vertical asymptotes of the curve ?
|
A. 0 |
|---|
| B. 1 |
C.  |
D. 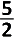 |
E. 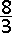 |
Oplossing - Solution
\(y=\frac{2}{x-1}+\frac{2}{4-x}=\frac{2(4-x)+2(x-1)}{(x-1)(4-x)}=\frac{8-2x+2x-2}{(x-1)(4-x)}=\frac{6}{(x-1)(4-x)} \)
De functie heeft dus twee verticale asymptoten (x = 1 en x = 4) en heeft daartussen een positieve (y) waarde. De afgeleide van y is
\(y'=-\frac6{(x-1)^2(4-x)^2}.(4-x-x+1)=\frac{6(2x-5)}{(x-1)^2(4-x)^2} \)
met nulwaarde x = \(\frac52\),
is negatief tussen 1 en \(\frac52\) en positief tussen \(\frac52\) en 4.
De functie gaat dus van dalen over naar stijgen en heeft dus inderdaad een minimum voor \(x=\frac52 \).
De y waarde in dat punt is \(\frac{6}{(\frac{5}{2}-1)(4-\frac{5}{2})}=\frac{6}{\frac32.\frac32}=6.\frac49=\frac83\)