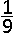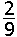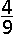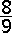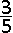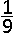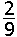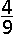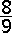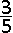Alex heeft vijf verschillend paar sokken mee op sportkamp genomen. Bij thuiskomst blijkt na de was dat er twee sokken (van de 10) ontbreken.
In het beste geval heeft hij nog vier paar sokken maar wat is de kans dat hij maar drie volledige stellen sokken overhoudt ?
|
A. 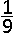 |
|---|
B. 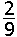 |
C. 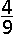 |
D. 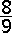 |
E. 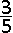 |
[ 6-7942 - op net sinds 19.7.15-()-4.12.2023 ]
Translation in E N G L I S H
|
IN CONSTRUCTION
|
A. |
|---|
| B. |
| C. |
| D. |
| E. |
Oplossing - Solution
1ste manier : rechtstreeks (niet via de complementaire gebeurtenis)
De kans dat de twee sokken NIET van eenzelfde paar zijn is
\(\frac{C_5^2.2.2}{C_{10}^{\,2}}=\frac{5.4.2.2}{10.9}=\frac89\)
De teller is afkomstige van een samengestelde beslissing die ontstaan is uit :
→ een eerste deelbeslissing : kies twee van de vijf paar (C52)
→ een tweede deelbeslissing : kies van elk van de twee paar de kous die verloren
is gegaan (2×2)
2de manier : via de complementaire gebeurtenis
Ofwel kunnen er drie, dan wel vier paar sokken gevormd worden.
De kans om drie volledige stellen te hebben is dus 1 min de kans om vier volledige stellen
te hebben.
Die (laatste) kans is \(\frac{5}{C_{10}^2}=\frac{5.2}{10.9}=\frac19\) (5 omdat er 5 paar sokken zijn)
De gevraagde kans is dus \(1-\frac19=\frac89\)