spreekt voor zichzelf.
Een diagonaal - tevens symmetrieas - zorgt ervoor dat er twee hoeken met grootte α en twee hoeken met grootte β te zien zijn (2α + 2β = 90°).
De tangens van α is duidelijk gelijk aan ½ , maar hoe groot is tan β ?



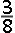
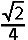
|
spreekt voor zichzelf. Een diagonaal - tevens symmetrieas - zorgt ervoor dat er twee hoeken met grootte α en twee hoeken met grootte β te zien zijn (2α + 2β = 90°). De tangens van α is duidelijk gelijk aan ½ , maar hoe groot is tan β ? |
A.  |
|---|---|
B.  | |
C.  | |
D. 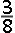 | |
E. 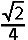 |
[ 5-7915 - op net sinds 23.9.15-(e)-15.9.2025 ]
|
IN CONSTRUCTIOn Value of tan β |
A. |
|---|---|
| B. | |
| C. | |
| D. | |
| E. |
