Voor welke
positieve a is de oppervlakte omsloten door de parabolen y = ax2 en x = ay2 precies gelijk aan 1 ?
positieve a is de oppervlakte omsloten door de parabolen y = ax2 en x = ay2 precies gelijk aan 1 ?


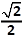

|
Voor welke
positieve a is de oppervlakte omsloten door de parabolen y = ax2 en x = ay2 precies gelijk aan 1 ? |
A. 1 |
|---|---|
B.  | |
C.  | |
D. 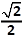 | |
E.  |
[ 6-7867 - op net sinds 9.2.15-()-16.11.2024 ]
| IN CONSTRUCTION |
|---|
