 vormt samen met de assen een gebied dat door y = sin x in twee delen wordt verdeeld.
vormt samen met de assen een gebied dat door y = sin x in twee delen wordt verdeeld.Wat is de verhouding van de oppervlakten van deze twee gebieden ( groot tot klein) ?



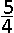
 vormt samen met de assen een gebied dat door y = sin x in twee delen wordt verdeeld. vormt samen met de assen een gebied dat door y = sin x in twee delen wordt verdeeld.Wat is de verhouding van de oppervlakten van deze twee gebieden ( groot tot klein) ? |
A. 1,5 |
|---|---|
B.  | |
C.  | |
D.  | |
E. 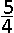 |
[ 6-7865 - op net sinds 4.2.15-(e)-6.12.2024 ]
| IN CONSTRUCTIOn y cos x y = sin x Ratio green to yellow |
A. 1,5 |
|---|---|
B.  | |
C.  | |
D.  | |
E. 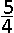 |
