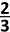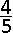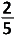Een zak bevat twee rode paprika's, vier groene en vier gele.
Zonder te kijken nemen we vier paprika's uit de zak.
Een zak bevat twee rode paprika's, vier groene en vier gele.
Zonder te kijken nemen we vier paprika's uit de zak.
Wat is de kans dat ze alle vier groen of geel zijn ?
|
A.  |
|---|
B.  |
C. 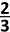 |
D. 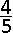 |
E. 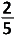 |
[ 6-7723 - op net sinds 31.1.2020-(E)-22.10.2023 ]
Translation in E N G L I S H
IN CONSTRUCTION
|
A. |
|---|
| B. |
| C. |
| D. |
| E. |
Oplossing - Solution
1ste manier :
Vier paprika's kiezen uit tien kan op C104 (noemer in de formule van LAPLACE)
De 'gunstige' gevallen krijgen we als we uit de acht gele of groene er vier uit kiezen :
dit kan op C84 manieren (teller in de formule van LAPLACE)
De kans is bijgevolg C84 / C104 = (8.7.6.5) / (10.9.8.7) = (6.5) / (10.9) = 6 / (2.9) = 1/3.
2de manier :
We passen de uitgebreide productwet toe [ de eenvoudige is P(A B)=P(A).P(B|A) ].
8/10 is de kans dat de eerst getrokken paprika geel of groen is
7/9 is de kans dat de tweede getrokken paprika geel of groen is, in de veronderstelling dat de eerste al geel of groen was
6/8 is de kans dat de derde getrokken paprika geel of groen is, in de veronderstelling dat de eerste twee al geel of groen waren
5/7 is de kans dat de vierde getrokken paprika geel of groen is, in de veronderstelling dat de eerste drie al geel of groen waren
Door het product te maken van die vier breuken krijgen we precies dezelfde breuk als in de 1ste manier, en uiteraard dus ook 1/3 als uitkomst

 Een zak bevat twee rode paprika's, vier groene en vier gele.
Zonder te kijken nemen we vier paprika's uit de zak.
Een zak bevat twee rode paprika's, vier groene en vier gele.
Zonder te kijken nemen we vier paprika's uit de zak.

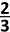
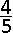
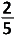
 Een zak bevat twee rode paprika's, vier groene en vier gele.
Zonder te kijken nemen we vier paprika's uit de zak.
Een zak bevat twee rode paprika's, vier groene en vier gele.
Zonder te kijken nemen we vier paprika's uit de zak.