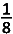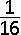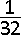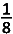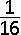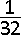Twee hoeken van een driehoek meten 15° en 75°. De gemeenschappelijke zijde (benen) van deze twee hoeken heeft lengte 1.

Hoe groot is de hoogte van
de driehoek naar deze zijde ? 		A.   1op2
B.   1op4
C.   1op8
D.   1op16
E.   1op32
A    B    C 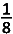   D 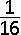   E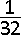

[ 5-7641 - op net sinds 22.10.14-()-27.10.2023 ]

Translation in   E N G L I S H

IN CONSTRUCTION A.  
B.  
C.  
D.  
E.  

Oplossing - Solution

De driehoek is rechthoekig en de gemeenschappelijke zijde is de schuine zijde met lengte 1.
Wegens de formule  a.h = b.c  is het voldoende het product van de rechthoekszijden te kennen want dat is dan gelijk aan de hoogte.
De twee rechthoekszijden hebben lengte sin 15° en sin 75°
(sinus scherpe hoek is   overstaande zijde / schuine zijde)
Het product ervan zal ons de dus de gevraagde hoogte opleveren.
h = sin15°.sin75° = sin15°.cos15° = ½.2.sin15°.cos15° = ½.sin30° = ¼