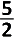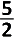De kleine basis wordt door het raakpunt met de cirkel verdeeld in twee gelijke lijnstukken met lengte 2.
De grote basis wordt door het raakpunt met de cirkel verdeeld in twee gelijke lijnstukken met lengte 4.
Daardoor worden de opstaande zijden door het raakpunt met de cirkel verdeeld in twee lijnstukken met lengte 2 en 4 en heeft dus zelf de lengte 6.
Door de loodlijn vanuit een hoekpunt van de kleine basis neer te laten op de grote basis, ontstaat een rechthoekige driehoek met schuine zijde
6
(de opstaande zijde van het trapezium) en rechthoekszijden 2r en 2 ( 2r = hoogte trapezium, 2 = ½ (8−4) )
Via de stelling van Pythagoras vinden we dan 6² = (2r)² + 2²
⇔ 36 = 4r² + 4 ⇔ 32 = 4r² ⇔ r² = 8 ⇔ r = 2
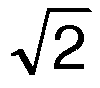
≈ 2,83