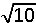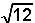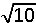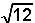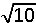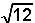1^ste manier :
De zwaartelijn (lengte x > 0) maakt hoeken α en 180° − α   met AB.
De cosinusregel "op 4 en 6" levert :
  4² = 4² + x² − 2.4.x.cos α
  6² = 4² + x² − 2.4.x.xos(180° − α)
Daar cos α en cos(180 − α ) tegengesteld zijn, levert dit na optelling
16 + 36 = 32 + 2x²  ⇔  52 = 32 + 2x²  ⇔  2x² = 20  ⇔  x² = 10  ⇔  x =
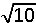2^de manier :
Er bestaat ook een formule om de zwaartelijnen te berekenen als je de lengte van de zijden kent : $m_a=\frac12\sqrt{2b^2+2c^2-2a^2}$.
Hier levert dit dus
$m_c=\frac12\sqrt{2a^2\!+2b^2\!-c^2}=\frac12\sqrt{2.4^2\!+\!2.6^2\!-\!8^2}=\frac12\sqrt{32\!+\!72\!-\!64}=\frac12.\sqrt{40}=\sqrt{10}$