|AC| = 5, |BC| = 3 trekt men
de zwaartelijn [CM]
(M midden van [AB]).
Hoe lang is die zwaartelijn ?

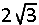
|
|AC| = 5, |BC| = 3 trekt men de zwaartelijn [CM] (M midden van [AB]). Hoe lang is die zwaartelijn ? |
A.  |
|---|---|
B. 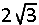 | |
| C. 3 | |
| D. 4 | |
| E. 5 |
[ 4-7612 - op net sinds 31.5.14-(E)-2.11.2023 ]
|
IN CONSTRUCTION |
A. |
|---|---|
| B. | |
| C. | |
| D. | |
| E. |