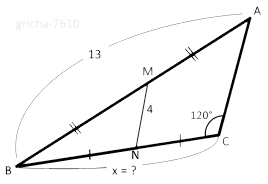
 In driehoek ABC is |AB|=13 en de hoek tegenover [AB] 120° .
Het lijnstuk [MN] dat het midden van [AB] en [BC] verbindt heeft lengte 4.
In driehoek ABC is |AB|=13 en de hoek tegenover [AB] 120° .
Het lijnstuk [MN] dat het midden van [AB] en [BC] verbindt heeft lengte 4.
Wat is de lengte van [BC] ?
|
A. 6 |
|---|
| B. 7 |
| C. 8 |
| D. 8,5 |
| E. 9 |
[ 4-7610 - op net sinds 4.8.2020-(E)-16.8.2024 ]
Translation in E N G L I S H
Oplossing - Solution
[MN] is de middenparallel van driehoek BCA. Bijgevolg is niet alleen MN//AC maar ook |AC| = 2.|MN| = 2.4 = 8.
We kennen dus drie elementen van driehoek ABC → ZZH.
ZZH is geen congruentiekenmerk wat voor gevolg heeft dat er in theorie zowel 0, 1 als 2 oplossingen mogelijk zijn. Gezien 13 > 8 en de hoek in C stomp is zal er maar precies één oplossing zijn. Die oplossing vinden we door de cosinusregel toe te passen op de zijde tegenover C :
13² = 8² + x² − 2.8.x.cos120° Nu is cos 120° = −½ zodat
169 = 64 + x² + 8x of ook nog
x² + 8x − 105 = 0 en daar V(7) = 49+56-105 = 0
(x − 7)(x + 15) = 0
x = 7 ∨ x = − 15
De enige oplossing die we in aanmerking kunnen nemen is dus 7.

 In driehoek ABC is |AB|=13 en de hoek tegenover [AB] 120° .
Het lijnstuk [MN] dat het midden van [AB] en [BC] verbindt heeft lengte 4.
In driehoek ABC is |AB|=13 en de hoek tegenover [AB] 120° .
Het lijnstuk [MN] dat het midden van [AB] en [BC] verbindt heeft lengte 4. In driehoek ABC is |AB|=13 en de hoek tegenover [AB] 120° .
Het lijnstuk [MN] dat het midden van [AB] en [BC] verbindt heeft lengte 4.
In driehoek ABC is |AB|=13 en de hoek tegenover [AB] 120° .
Het lijnstuk [MN] dat het midden van [AB] en [BC] verbindt heeft lengte 4.