De parabool met vergelijking
y = x2 + bx − 1
heeft T als top en snijdt
de x-as in de punten A en B.
De oppervlakte van driehoek ABT
is  als b gelijk is aan als b gelijk is aan
|
A. 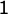 |
|---|
B. 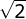 |
C. 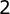 |
D. 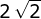 |
E. 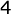 |
[ 4-7576 - op net sinds 11.11.13-(E)-8.11.2024 ]
Translation in E N G L I S H
The parabola with vertex T and
equation y = x2 + bx - 1
intersects de x-axis at A and B.
The area of traingle ABT is
 if b equals if b equals
|
A.  |
|---|
B. 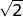 |
C. 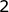 |
D. 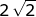 |
E. 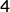 |
Oplossing - Solution
De afstand van A tot B (de twee snijpunten met de x-as) is
\(\left|x_1-x_2\right|=\left|\frac{-b+\sqrt D}{2}-\frac{-b-\sqrt D}{2}\right|=\left|\frac{-b+\sqrt D+b+\sqrt D}{2}\right|=\sqrt D=b^2+4\)
De absolute waarde van de ordinaat van de top T is tevens de hoogte van de driehoek en dus gelijk aan \(\left|-\frac{D}{4a}\right|=\frac{D}{4}\)
De oppervlakte van ΔABT is bijgevolg \(\frac{1}{2}.\sqrt D.\frac{D}{4}=\frac{\sqrt{D^3}}{8}=\frac{\sqrt{(b^2+4)^3}}{8}\)
De volgende vergelijking moet dus opgelost worden :
\(\frac{\sqrt{(b^2+4)^3}}{8}=2\sqrt2\;\Leftrightarrow\;\sqrt{(b^2+4)^3}=16\sqrt2=\sqrt{2^8}\sqrt2=\sqrt{2^9}\\
\Leftrightarrow\;(b^2+4)^3=2^9\;\Leftrightarrow\;b^2+4=2^3\;\Leftrightarrow\;b^2=4\;\Leftrightarrow\; b=\pm2\)
Het antwoord is dus C vermist b = −2 niet bij de alternatieven staat.