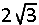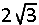1^ste manier :
De twee hoeken in D hebben een grootte van 60° en 120°.
De rechthoekige driehoek ABD heeft dus scherpe hoeken van 30° en 60°.
In Δ ABC is \(\tan30^\circ = \frac{|AB|}{|AC|}=\frac{|AB|}{12} \;\Rightarrow\; |AB|=12.\tan30^\circ =12.\frac{\sqrt3}{3}=4\sqrt3 \)
In Δ ABD is \(\cot60°=\frac{|AD|}{|AB|}=\frac{x}{4\sqrt3} \;\Rightarrow\; x=4\sqrt3.\cot60^\circ =4\sqrt3.\frac{\sqrt3}{3}=4\)
2^de manier :
Driehoek DBC is gelijkbenig, dus |BD| = 12 − x
De twee hoeken in D hebben een grootte van 60° en 120°.
In ΔABC is \(\tan30^\circ = \frac{|AB|}{|AC|}=\frac{|AB|}{12}\;\Rightarrow\;|AB|=12.\tan30^\circ =12.\frac{\sqrt3}{3}=4\sqrt33\)
In rechthoekige driehoek ABD passen we de stelling van Pythagoras toe :
(4)² + x² = (12 − x)²  ⇔  16.3 + x² = 144 − 24x + x²  ⇔  24x = 144 − 48 = 96
Bijgevolg is   x = 96 : 24 = . . .