y =
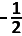 en
y =
en
y =  ?
?|
Wat is de oppervlakte van het deel van de goniometrische cirkel (schijf) dat begrensd wordt door de rechten y = 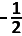 en
y = en
y =  ? ? |
A. \(\large\boldsymbol{\frac {\pi} {2} }\) | |
|---|---|---|
| B. \(\large\boldsymbol{\frac {\pi} {3} }\) | ||
| C. \(\large\boldsymbol{\frac {\pi} {3}-\frac{\sqrt 3}{2} }\) | ||
| D. \(\large\boldsymbol{\frac {\pi} {3}-\frac{\sqrt 3}{3} }\) | ||
| E. \(\large\boldsymbol{\frac {\pi} {3}+\frac{\sqrt 3}{2} }\) |
[ 4-7536 - op net sinds 14.8.14-(E)-4.11.2024 ]
|
Circle with radius 1.
Lines y = − ½ and y = ½ What is the area of the green region ? |
A. \(\boldsymbol{\frac {\pi} {2} }\) | |
|---|---|---|
| B. \(\boldsymbol{\frac {\pi} {3} }\) | ||
| C. \(\boldsymbol{\frac {\pi} {3}-\frac{\sqrt 3}{2} }\) | ||
| D. \(\boldsymbol{\frac {\pi} {3}-\frac{\sqrt 3}{3} }\) | ||
| E. \(\boldsymbol{\frac {\pi} {3}+\frac{\sqrt 3}{2} }\) |
