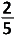 van de kans om een zwarte bal te trekken.
van de kans om een zwarte bal te trekken.Wat is de kans om een zwarte bal te trekken ?
Een zak bevat zwarte en witte ballen. De kans om een witte bal te trekken is 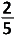 van de kans om een zwarte bal te trekken. van de kans om een zwarte bal te trekken.Wat is de kans om een zwarte bal te trekken ? |
A. \(\frac25\) |
|---|---|
| B. \(\frac27\) | |
| C. \(\frac35\) | |
| D. \(\frac57\) | |
| E. \(\frac37\) |
[ 6-7435 - op net sinds 19.8.2020-(E)-6.5.2025 ]
|
IN CONSTRUCTION |
|---|
