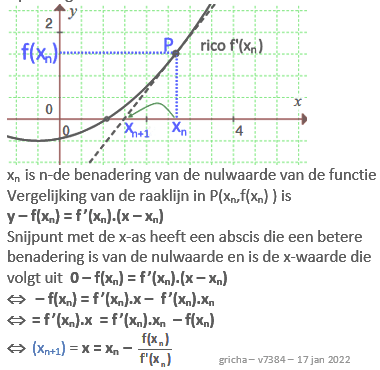
|
Als xn een benadering is van de
nulwaarde van f (x), dan is volgens de NEWTON-RAPHSON methode xn+1
een volgende en betere benadering. Volgens die methode moet |
A. \(\boldsymbol{x_{n+1}=x_n-\frac {f\,(x_n)} {f'(x_n)} }\) |
|---|---|
| B. \(\boldsymbol{x_{n+1}=x_n+\frac {f\,(x_n)} {f'(x_n)} }\) | |
| C. \(\boldsymbol{x_{n+1}=x_n-\frac {f'(x_n)} {f\,(x_n)} }\) | |
| D. \(\boldsymbol{x_{n+1}=x_n+\frac {f'(x_n)} {f\,(x_n)} }\) | |
| E. \(\boldsymbol{x_{n+1}=\frac {f\,(x_n)} {f'(x_n)}-x_n }\) |
[ 5-7384 - op net sinds 27.1.14-(E)-18.11.2023 ]
| IN CONSTRUCTION | A. |
|---|---|
| B. | |
| C. | |
| D. | |
| E. |

