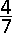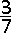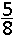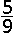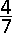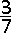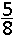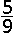Men werpt een dobbelsteen met zes vlakken waarop 1, 2, 3, 4, 5, 6 stippen staan.
De kans dat een bepaald vlak boven komt is evenredig met het aantal stippen dat erop staat (dus een zes gooien maakt de meeste kans, een één gooien de minste kans).
Wat is de kans om een even getal te verkrijgen bij één worp ?
|
A. 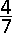 |
|---|
B. 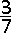 |
C. 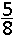 |
D. 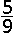 |
E.  |
[ 6-7244- op net sinds 21.3.13-()-3.11.2023 ]
Translation in E N G L I S H
|
IN CONSTRUCTION
|
A. |
|---|
| B. |
| C. |
| D. |
| E. |
Oplossing - Solution
Stel p de kans om een 1 te gooien (de kleinste kans).
Dan zijn de kansen om een 2 te gooien 2p, een drie 3p, ... enz.
Immers de kansen moeten evenredig zijn met 1,2,3,4,5,6.
Daar de som van alle elementaire gebeurtenissen 1 moet zijn geldt er : p + 2p + 3p + 4p + 4p + 6p = 1 ⇔ 21p = 1 ⇔ p = 1/21
De zes kansen zijn dus \(\boldsymbol{\frac {1} {21},\; \frac {2} {21},\;...,\frac {6} {21}}\)
De kans om een even aantal ogen te gooien is dus \(\boldsymbol{\frac {2} {21}\;+\frac {4} {21}\;+\frac {6} {21}\;=\frac {12} {21}\;=\;...}\)