in 1 en 3, de y-as in 12.
Anders gezegd : (1,0), (3,0) en (0,12)
zijn drie punten van de parabool.
Deze parabool is congruent
met de grafiek van
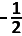 x2
x2|
Een parabool snijdt de x-as in 1 en 3, de y-as in 12. Anders gezegd : (1,0), (3,0) en (0,12) zijn drie punten van de parabool. Deze parabool is congruent met de grafiek van |
A. y = x2 |
|---|---|
| B. y = 2x2 | |
| C. y = 3x2 | |
| D. y = 4x2 | |
E. y = 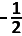 x2 x2 |
[ 4-7216 - op net sinds 18.5.13-()-4.11.2023 ]
| IN CONSTRUCTION | A. |
|---|---|
| B. | |
| C. | |
| D. | |
| E. |