=)
|
A. 1 |
|---|
| B. 2 |
| C. 3 |
| D. 4 |
E. 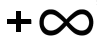 |
[ 6-7067 - op net sinds 19.2.2022-(E)-3.11.2023 ]
Translation in E N G L I S H
=)
|
A. 1 |
|---|
| B. 2 |
| C. 3 |
| D. 4 |
| E. ∞ |
Oplossing - Solution
De limiet van de eerste breuk is gelijk aan 2.
We berekenen nu de limiet van de tweede breuk :
\(
\displaystyle \lim_{\underset{>}{x \to {0}}}\left ( \frac{\log\; \sin {2x}}{\log\; \sin x} \right )\left ( =\frac00 \right )\overset{H}{=}\displaystyle \lim_{\underset{>}{x \to {0}}}\frac{\frac{1}{\ln10.\sin2x}.2.\cos {2x}}{\frac{1}{\ln 10.\sin x}.\cos x}\\=\displaystyle \lim_{\underset{>}{x \to {0}}} \frac{2.\sin x.\cos {2x}}{\sin 2x.\cos x}=
\displaystyle \lim_{x \to 0} \frac{\frac{\sin x}{x}}{\frac{\sin{2x}}{2x}}\cdot
\displaystyle \lim_{x \to 0} \frac{\cos {2x}}{\cos x} =\frac11\cdot \frac 11=1
\)
Nu nog de som maken van deze twee limieten.