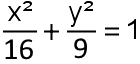 wordt door de parabool y² = 2px gesneden in twee punten A en B die samen met hun spiegelbeeld t.o.v.de y-as een vierkant vormen.
wordt door de parabool y² = 2px gesneden in twee punten A en B die samen met hun spiegelbeeld t.o.v.de y-as een vierkant vormen.De vergelijking van die parabool is dan
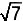 x
x
De ellips 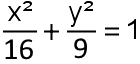 wordt door de parabool y² = 2px gesneden in twee punten A en B die samen met hun spiegelbeeld t.o.v.de y-as een vierkant vormen. wordt door de parabool y² = 2px gesneden in twee punten A en B die samen met hun spiegelbeeld t.o.v.de y-as een vierkant vormen.De vergelijking van die parabool is dan |
A. y² = 1,2 x |
|---|---|
| B. y² = 2,4 x | |
| C. y² = 4,8 x | |
| D. y² = 9,6 x | |
E. y² = 4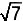 x x |
[ 6-7038 - op net sinds 13.7.2020-(E)-22.10.2023 ]
|
IN CONSTRUCTION |
|---|
