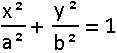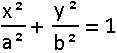Van de ellips ellips is T de top T(0,b).  F' en F zijn de brandpunten, gelegen op de x-as.
De excentriciteit e van de ellips is precies  ½  als de hoek tussen TF' en TF gelijk is aan 		A.  90°
B.  60°
C.  45°
D.  30°
E.  geen van
   de vorige
A    B    C    D    E 

[ 6-7029 - op net sinds 30.5.12-(E)-29.10.2023 ]

Translation in   E N G L I S H

T(0,b) is the top of the ellipse 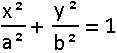ellips
F' and F' are foci of the ellipse.
If the eccentricity of the ellipse is ½
how large is the angle between TF' and TF ?
A.  90°
B.  60°
C.  45°
D.  30°
E.  none of the
  above

Oplossing - Solution

De excentriciteit e van een ellips is gelijk aan de breuk c/a.
De hoek tussen TF' en TF is 60°.
Dan is de driehoek OTF een rechthoekige driehoek met scherpe hoeken van 30° en 60° zodat de langste zijde (|TF| = a) gelijk is aan het dubbel van de kortste zijde (|OF| = c).
Dus a = 2c  ⇔  \(\frac ca = \frac 12 \)
gricha