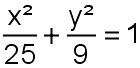 is een rechthoek ingeschreven waarvan de zijden evenwijdig zijn
met de assen en waarbij de twee kortste zijden door de twee brandpunten gaan.
is een rechthoek ingeschreven waarvan de zijden evenwijdig zijn
met de assen en waarbij de twee kortste zijden door de twee brandpunten gaan.Deze kortste zijden hebben elk een lengte van
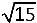
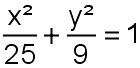 is een rechthoek ingeschreven waarvan de zijden evenwijdig zijn
met de assen en waarbij de twee kortste zijden door de twee brandpunten gaan.
is een rechthoek ingeschreven waarvan de zijden evenwijdig zijn
met de assen en waarbij de twee kortste zijden door de twee brandpunten gaan.Deze kortste zijden hebben elk een lengte van |
A. 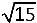 |
|---|---|
| B. 2 | |
| C. 3 | |
| D. 4 | |
| E. 3,6 |
[ 6-6952 - op net sinds 4.5.15-()-23.6.2025 ]
|
IN CONSTRUCTION Length of one side of rectangle. |
A. |
|---|---|
| B. | |
| C. | |
| D. | |
| E. |
