|
De rechte door het brandpunt en loodrecht op de positieve x-as van de hyperbool
\(\boldsymbol{\frac {x^2} {16} - \frac {y^2} {9} = 1 }\) snijdt de hyperbool in twee punten.
Eén ervan is D. De raaklijn in D snijdt de x-as in het punt met abscis
|
A. 1,6 |
|---|
| B. 2,25 |
| C. 3,2 |
| D. 4 |
E. 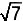 |
| F. − 5 |
[ 6-6590 - op net sinds 20.5.13-(e)-4.11.2023 ]
Translation in E N G L I S H
|
IN CONSTRUCTION
|
A. |
|---|
| B. |
| C. |
| D. |
| E. |
Oplossing - Solution
Voor de hyperbool \(\frac{x^2}{16}-\frac{y^2}{9}=1\) is a = 4 en b = 3
zodat c² = a² + b² = 16 + 9 = 25 en dus c = 5.
De rechte door het brandpunt en loodrecht op de x-as heeft dus als vergelijking x = 5
en snijdt de hyperbool in (5, y1). De raaklijn in dat punt aan de hyperbool heeft als
vergelijking \(\frac{5x}{16}-\frac{y_1y}{9}=1\) en snijdt de x-as in een punt met abscis die volgt uit \(\frac{5x}{16}-\frac09=1\).
Bijgevolg is \(\frac{5x}{16}=1\;\Leftrightarrow\;5x=10\;\Leftrightarrow\;x=\frac{16}{5}=\frac{32}{10}=3,2\).
Merk op dat we het snijpunt (x1,y1) van x = 5 met de hyperbool niet precies hoeven te kennen
wat de berekeningen nagenoeg halveert !