Wat is het bereik
van de functie
=\frac{x^2}{x^2+4})
van de functie
 ]
]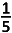 ]
]|
Wat is het bereik
van de functie |
A. [ 0, 1 [ |
|---|---|
| B. [ 0, | |
| C. | |
D. [ 0,  ] ] | |
E. [ 0, 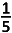 ] ] |
[ 5-6535 - op net sinds 19.11.2021-(E)-21.8.2025 ]
|
What is the range of the functrion |
A. [ 0, 1 ) |
|---|---|
| B. [ 0, | |
| C. | |
| D. [ 0, | |
| E. [ 0, |
 is en dat 1 zeker NIET tot het bereik behoort ( y ≠ 1 ).
is en dat 1 zeker NIET tot het bereik behoort ( y ≠ 1 ).