verzameling
van
is
|
De oplossingen- verzameling van is |
A. |
|---|---|
| B. | |
| C. | |
| D. ] − 3, 0 [ ∪ ] 0, 3 [ | |
| E. | |
| F. leeg ( ∅ ) |
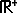 = { x | x ≥ 0 }
= { x | x ≥ 0 }
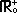 = { x | x > 0 }
= { x | x > 0 }
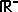 = { x | x ≤ 0 }
= { x | x ≤ 0 }
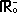 ={ x | x < 0 }
={ x | x < 0 }
[ 5-6410 - op net sinds 18.4.13-(E)-4.11.2024]
|
What is the solutionset of is IN CONSTRUCTION |
A. |
|---|---|
| B. | |
| C. | |
| D. | |
| E. |
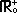 (de noemer x mag niet nul zijn)
(de noemer x mag niet nul zijn)