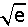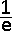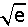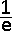\( \displaystyle\lim_{x\rightarrow +\infty} \left ( \frac{x-2}{x-1} \right )^{x-1} =\lim_{x\rightarrow +\infty} \left ( \frac{x-1-1}{x-1} \right )^{x-1} =\lim_{x\rightarrow +\infty} \left ( 1+\frac{1}{1-x} \right )^{x-1} \)
\(=\displaystyle\lim_{x\rightarrow +\infty} \left ( 1+\frac{1}{1-x} \right )^{(1-x).\frac{x-1}{1-x}} =e^{\left (\displaystyle\lim_{x\rightarrow +\infty} \frac{x-1}{1-x} \right )}=e^{-1}=\frac{1}{e} \)