Het stelsel

is strijdig voor
de volgende waarde
van de parameter m :
is strijdig voor
de volgende waarde
van de parameter m :
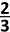

|
Het stelsel
is strijdig voor de volgende waarde van de parameter m : |
A. 1 |
|---|---|
| B. 2 | |
C. 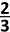 | |
| D. 0 | |
E.  |
[ 5-6119 - op net sinds 12.11.12-(E)-24.8.2025 ]
|
The system is inconsistent for the following value of the parameter m : |
A. 1 |
|---|---|
| B. 2 | |
| C. | |
| D. 0 | |
| E. |
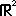 is.
is.