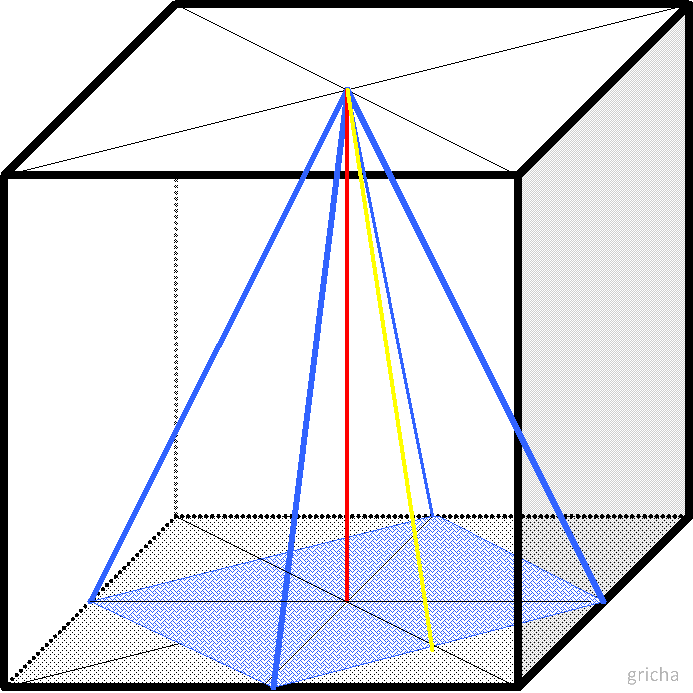
 In een kubus met ribbe 4 is een piramide met hoogte 4 getekend waarvan het grondvlak een vierkant is dat de middens verbindt van de zijden van het grondvlak van de kubus.
In een kubus met ribbe 4 is een piramide met hoogte 4 getekend waarvan het grondvlak een vierkant is dat de middens verbindt van de zijden van het grondvlak van de kubus.Hoe lang is elk van de vier de opstaande ribben van de piramide ?

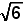
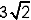
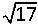
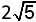
 In een kubus met ribbe 4 is een piramide met hoogte 4 getekend waarvan het grondvlak een vierkant is dat de middens verbindt van de zijden van het grondvlak van de kubus.
In een kubus met ribbe 4 is een piramide met hoogte 4 getekend waarvan het grondvlak een vierkant is dat de middens verbindt van de zijden van het grondvlak van de kubus.Hoe lang is elk van de vier de opstaande ribben van de piramide ? |
A. 4  |
|---|---|
B. 2 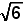 | |
C. 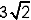 | |
D. 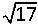 | |
E. 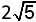 |
[ 4-5954 - op net sinds 1.4.2020-(E)-2.11.2023 ]
|
IN CONSTRUCTION |
A. 4  |
|---|---|
B. 2 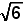 | |
C. 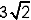 | |
| D. \(\sqrt {17} \) | |
E. 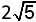 |
