Hoe groot is de verhouding van de inhoud van de kubus tot de inhoud van de kegel ?
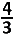
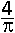
|
Hoe groot is de verhouding van de inhoud van de kubus tot de inhoud van de kegel ? |
A. \(\frac {12} {\pi} \) |
|---|---|
B. 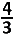 | |
| C. π | |
| D. 4 | |
E. 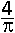 |
[ 4-5951- op net sinds 14.2.13-()-4.11.2023 ]
|
IN CONSTRUCTION |
|---|
