1^ste manier :
De oppervlakte van de cirkelsector is precies één derde van de oppervlakte van de cirkel, dus  \(\frac13.\pi r^2=\frac13\pi.(3\;cm)^2=\frac13.\pi.9\;cm^2 = 3\pi\;cm^2\)
2^de manier : (vanaf 5de jaar)
S = θ r²  is de formule voor de oppervlakte van een cirkelsector als de openingshoek θ in radialen is uitgedrukt.
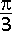
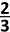
Daar 180° = π rad  ⇔  60° = rad  ⇔  120° = π rad   verkrijgen we
\(S=\frac12\frac23\pi.(3\;cm)^2=\frac13.\pi.9\;cm^2 = 3\pi \;cm^2\)
3^de manier : (vanaf 5de jaar)
In een cirkel met straal R is er een eenvoudig verband tussen de middelpuntshoek θ en de bijbehorende boog met lengte   L →  L = θR  (eenvoudiger kan niet !). Voorwaarde is wel dat de hoek in radialen* wordt uitgedrukt.
Meer nog : je kan (en mag) een cirkelsector beschouwen als een driehoek (!) met basis L en hoogte R en de formule toepassen voor de oppervlakte van een driehoek die je geleerd hebt in de basisischool :   \(S=\frac{L.R}{2}\).
In ons geval wordt dat  \(\theta=\frac23\pi\) (rad)  zodat  \(L=\theta R=\frac23\pi.3\;cm=2\pi\;cm\) en \(S = \frac {(2\pi\;cm).(3\;cm)} {2} =3\pi\;cm^2\)
* Hier hebben we een voorbeeld van het nut van radialen : formules worden er meestal eenvoudiger door