Gezien de wortelvorm zijn alle oplossingen positief (als er zijn) en gezien de noemer is 2 ook zeker geen oplossing.
Laat ons nu die positieve getallen verdelen in de intervallen [0, 2[  en  ]2,[
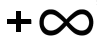
a) voor x ∈ [0, 2[ is de teller negatief alsook de noemer
    Het interval [0, 2[ behoort dus al zeker tot de oplossingenverzameling.
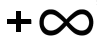
b) voor x ∈ ]2,[ is de noemer negatief.
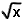
    De bijkomende oplossingen zijn dus deze die de teller strikt poistief maken :     − 3 > 0  ⇔  > 0  ⇔  x > 9
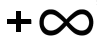
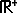
Besluit : de oplossingenverzameling is [0, 2[ ∪ ]9, [ = \ [ 2, 9 ]