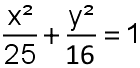 en
ende vlieger met twee rechte hoeken, spreekt voor zichzelf.
De langste diagonaal van de vlieger heeft een lengte van
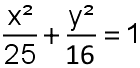 en ende vlieger met twee rechte hoeken, spreekt voor zichzelf. De langste diagonaal van de vlieger heeft een lengte van |
A. 10 |
|---|---|
| B. 2,25 | |
| C. 10,25 | |
| D. 9 | |
| E. 12 |
[ 6-5581 - op net sinds 5.1.2021-(e)-21.6.2025 ]
|
two right angles Elipse Length [BP] is ... IN CONSTRUCTION |
A. 10 |
|---|---|
| B. 2.25 | |
| C. 10.25 | |
| D. 9 | |
| E. 12 |
