is gelijk aan
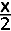 + C
+ C cos x + C
cos x + C cos x + C
cos x + C|
De onbepaalde integraal is gelijk aan |
A. − cos 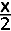 + C + C |
|---|---|
B. −  cos x + C cos x + C | |
C. −  cos x + C cos x + C | |
| D. − cos x + C | |
| E. \(\ln \frac {1} {\cos^2\frac x2} \) + C |
[ 6-5577 - op net sinds 15.6.11-(E)-4.11.2023 ]
| Evaluate the indefinite integral |
A. − cos 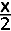 + C + C |
|---|---|
| B. − | |
| C. − | |
| D. − cos x + C | |
| E. \(\ln \frac {1} {\cos^2\frac x2} \) + C |