twee kubussen met
ribbe 1 (zie figuur).
De lengte van de lichaamsdiagonaal van deze balk (m.a.w. de afstand van A tot B) bedraagt


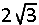
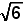
|
twee kubussen met ribbe 1 (zie figuur). De lengte van de lichaamsdiagonaal van deze balk (m.a.w. de afstand van A tot B) bedraagt |
A.  |
|---|---|
| B. 2 | |
| C. 3 | |
D.  | |
E. 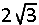 | |
F. 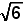 |
[ 4-5272 - op net sinds 16.2.2020-(E)-30.10.2023 ]
|
IN CONSTRUCTION |
|---|
