Voor de hoek α tussen de twee rode rechten geldt :
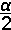 =
= 
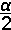 =
= 
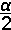 =
= 
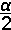 =
= 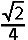
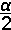 =
= 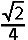
|
Voor de hoek α tussen de twee rode rechten geldt : |
A. sin 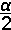 = =  |
|---|---|
B. cos 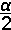 = =  | |
C. tan 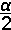 = =  | |
D. cos 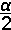 = = 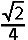 | |
E. sin 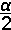 = = 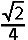 |
[ 4-5102 - op net sinds 9.2.13-(e)-7.12.2024 ]
|
IN CONSTRUCTION Which formula is correct ? |
|---|
