(tot x = k) wentelt rond de x-as, krijg je een (deel van een) paraboloïde die precies "past" in de getekende omschreven cilinder.
Welk volumedeel van de cilinder wordt door de paraboloïde ingenomen ?
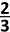



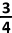
|
(tot x = k) wentelt rond de x-as, krijg je een (deel van een) paraboloïde die precies "past" in de getekende omschreven cilinder. Welk volumedeel van de cilinder wordt door de paraboloïde ingenomen ? |
A. 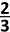 |
|---|---|
B.  | |
C.  | |
D.  | |
E. 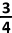 |
[ 6-4844 - op net sinds 21.1.14-(e)-28.7.2024]
| IN CONSTRUCTION What part of the cylinder is occupied by the paraboloid ? |
A. |
|---|---|
| B. | |
| C. | |
| D. | |
| E. |
