De blauwe hyperbool heeft als vergelijking
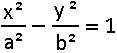.De rode hyperbool heeft dezelfde asymptoten als de zwarte en heeft dus als vgl.
|
De blauwe hyperbool heeft als vergelijking 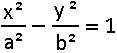.De rode hyperbool heeft dezelfde asymptoten als de zwarte en heeft dus als vgl. |
A. \(\large\boldsymbol{\frac{x^2}{a^2} - \frac{y^2}{b^2}} = -1\) |
|---|---|
| B. \(\large\boldsymbol{\frac{x^2}{a^2} + \frac{y^2}{b^2}} = 1\) | |
| C. \(\large\boldsymbol{\frac{x^2}{a^2} + \frac{y^2}{b^2}} = -1\) | |
| D. \(\large\boldsymbol{\frac{x^2}{b^2} - \frac{y^2}{a^2}} = 1\) | |
| E. \(\large\boldsymbol{\frac{x^2}{b^2} - \frac{y^2}{a^2}} = -1\) |
[ 6-4810 - op net sinds 2.5.06-(E)-26.11.2023 ]
|
The black hyperbola has the equation .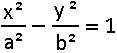
The red hyperbola has thesame asymptotes as the black one. The equation of the red hyperbola is |
A. \(\large\boldsymbol{\frac {x^2} {a^2} - \frac {y^2} {b^2}} = -1 \) |
|---|---|
| B. \(\large\boldsymbol{\frac {x^2} {a^2} + \frac {y^2} {b^2}} = 1 \) | |
| C. \(\large\boldsymbol{\frac {x^2} {a^2} + \frac {y^2} {b^2}} = -1 \) | |
| D. \(\large\boldsymbol{\frac {x^2} {b^2} - \frac {y^2} {a^2}} = 1 \) | |
| E. \(\large\boldsymbol{\frac {x^2} {b^2} - \frac {y^2} {a^2}} = -1 \) |
