1ste manier :
y = x − 2 snijpunt met de x-as is ( 2, 0 ) afstand tot oorsprong is 2
snijpunt met de y-as is ( 0,−2 ) afstand tot oorsprong is 2
y = 2x − 2 snijpunt met de x-as is ( 1, 0 ) afstand tot oorsprong is 1
snijpunt met de y-as is (0,−2) afstand tot oorsprong is 2
y =

(x − 1) snijpunt met de x-as is ( 1, 0 ) afstand tot oorsprong is 1
snijpunt met de y-as is ( 0,
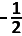
) afstand tot oorsprong is ?
y = 4x + 4 snijpunt met de x-as is ( −

, 0 ) afstand tot oorsprong is
snijpunt met de y-as is ( 0, 4 ) afstand tot oorsprong is 4
y =

x + 2 snijpunt met de x-as is (− 4 0) afstand tot oorsprong is 4
snijpunt met de y-as is ( 0, 2 ) afstand tot oorsprong is 2
→ Je ziet dus dat het reeds in het begin "bingo" is.
2de manier :
Als het snijpunt met de x-as even ver moet liggen als het snijpunt met de y-as,
dan kan het niet anders zijn dat de rechte evenwijdig is met de 1
ste of de 2
de bissectrice.
De richtingscoëfficiënt van de rechte moet dus +1 of −1 zijn.
Het is duidelijk dat er maar één rechte is die hieraan voldoet.
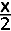 + 2
+ 2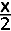 + 2
+ 2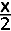 + 2
+ 2