is |
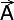 | = 3 en |
| = 3 en |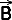 | = 5.
| = 5.Als je weet dat beide vectoren
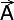 en
en 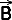 loodrecht op elkaar staan,
loodrecht op elkaar staan,dan is de nulvector ook gelijk aan
|
In een orthonormaal assenstelsel is | 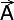 | = 3 en | | = 3 en |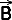 | = 5. | = 5.Als je weet dat beide vectoren 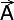 en en 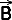 loodrecht op elkaar staan, loodrecht op elkaar staan,dan is de nulvector ook gelijk aan |
A. \(\vec A^2.\vec B^2\) |
|---|---|
| B. \((\vec A.\vec B)^2\) | |
| C. \((3\vec A).(5\vec B)\) | |
| D. \((\vec A.\vec B).\vec A\) | |
| E. \(5-(\sqrt5)^2\) |
[ 4-4590 - op net sinds 27.7.12-(E)-18.7.2024 ]
|
In a normal (orthogonal) Cartesian coordinate system is | 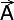 | = 3 en | | = 3 en |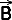 | = 5. | = 5.If you know that both vectors 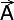 and and 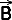 are perpendicular are perpendicularthen the nulvector is represented by |
A. \(\vec A^2.\vec B^2\) |
|---|---|
| B. \((\vec A.\vec B)^2\) | |
| C. \((3\vec A).(5\vec B)\) | |
| D. \((\vec A.\vec B).\vec A\) | |
| E. \(5-(\sqrt5)^2\) |
