tan x + 2cot x = 3
Het is duidelijk dat de getallen die tan x of cot x nul maken geen oplossing kunnen zijn, m.a. w. alle veelvouden van 90° zijn uitgesloten.(*) We vermenigvuldigen beide leden met tan x (wat het 'binnensmokkelen' van veelvouden van 180° kan meebrengen) en vervangen daarbij cot x. tan x door 1 (wat enkel juist is als x geen veelvoud is van 90°)
tan² x + 2 = 3.tan x
tan² x − 3.tan x + 2 = 0
y² − 3y + 2 = 0  ∧  tan x = y
(y − 1)(y − 2) = 0  ∧  tan x = y
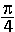
a) tan x = 1  ⇔  x = + k.π
b) tan x = 2  ⇔  x = Bgtan 2 + k.
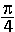
Opl = { + k.π, Bgtan 2 + k.π }   (rek. gehouden met *)
        of als je wil : {45° + k.180°, 63°26′6″ + k.180°}
In het interval  [ 0, 2π [  zijn er dus vier oplossingen.