Wiskunde Multiple Choice Vraag uit Gricha's Wiskundige Vragenbank

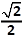
De hoogte h van een regelmatige p i r a m i d e, waarvan alle acht ribben lengte 2 hebben, is gelijk aan	A. 1
B. 2
C. 3
D.
E.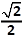
F. 1,5

What is the height of this pyramid ? All eight edges have length 2.	A. 1
	B. 2
	C. 3
	D.
	E.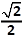
	F. 1.5

Een vierkant met zijde 2 heeft een diagonaal met lengte 2. v2puur

.
De halve diagonaal heeft dus een lengte van v2puur

.
De hoogte h is dan niets anders dan de lengte van de rechthoekszijde van een rechthoekige driehoek waarvan de schuine zijde 2 is en een rechthoekszijde v2puur

. Via de stelling van Pythagoras vinden we dat
h² = 2² − ( v2puur

)² = 4 − 2 = 2. De hoogte zelf heeft dus een lengte van ...